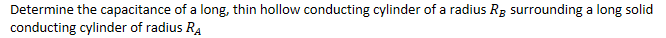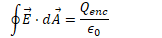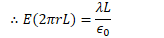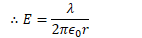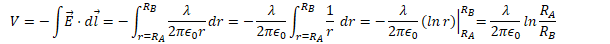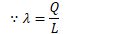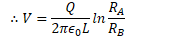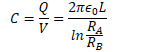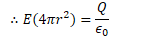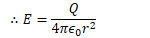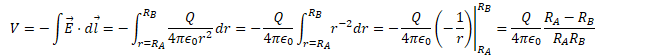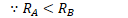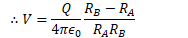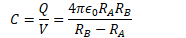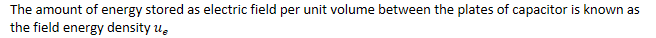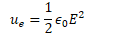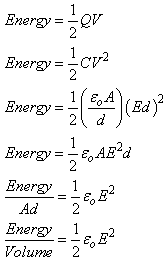What is a Capacitor?

• A capacitor is an electric device used to store electrical energy

  • Two conducting plates

  • Insulating material between (dielectric)

• Place opposite charges on each plate

• Develop a potential difference across the plates

• Energy is stored in the electric field between the plates

  

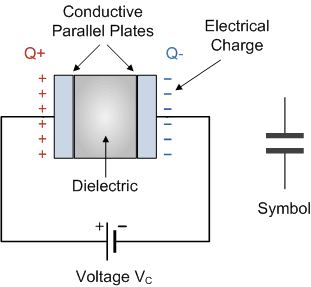
Capacitance

• Capacitance (C) is the ratio of the charge separated on the plates of a capacitor to the potential difference between the plates

• Units of capacitance are coulombs/volt, or farads (F)

  • A farad is a very large amount of capacitance

  

Calculating Capacitance

1. Assume a charge of +Q and -Q on each conductor

2. Find the electric field between the conductors (Gauss's Law)

3. 

4. 

Example 1: Parallel Plates

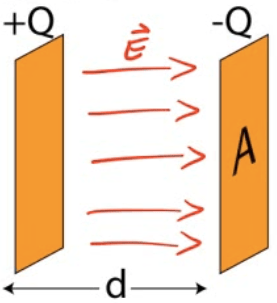
• Determine the capacitance between identical parallel plates of area A separated by a distance d

1. Assume +Q and -Q

2. 

3. 

   

   

4. 

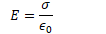
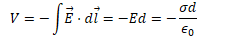
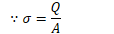
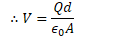
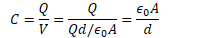
Example 2: Cylindrical Capacitor

1. Assume +Q and -Q

Example 3: Spherical Capacitor

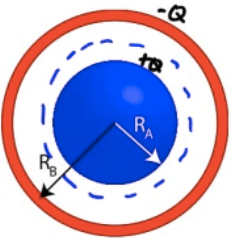
1. Assume +Q and -Q

Energy Stored in a Capacitor

• Work is done charging a capacitor, allowing the capacitor to store energy.

• 

• 

• 

• 

• 

  

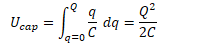
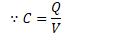
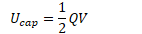
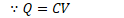
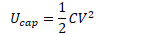
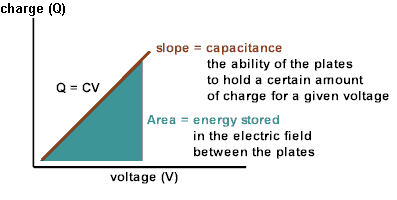
Field Energy Density

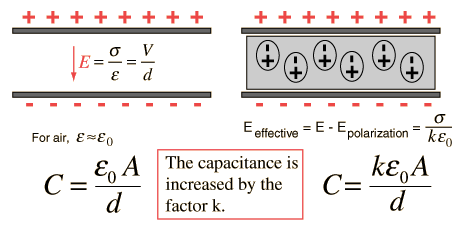
Dielectrics

• Insulating Materials

  

  

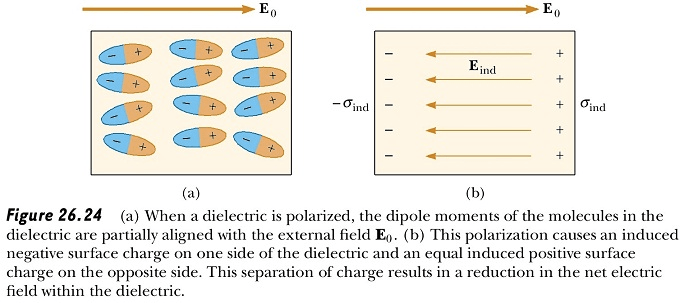
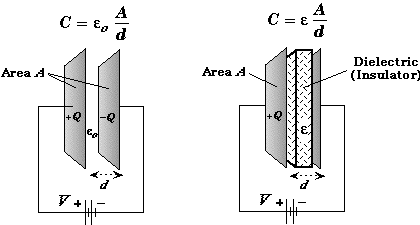
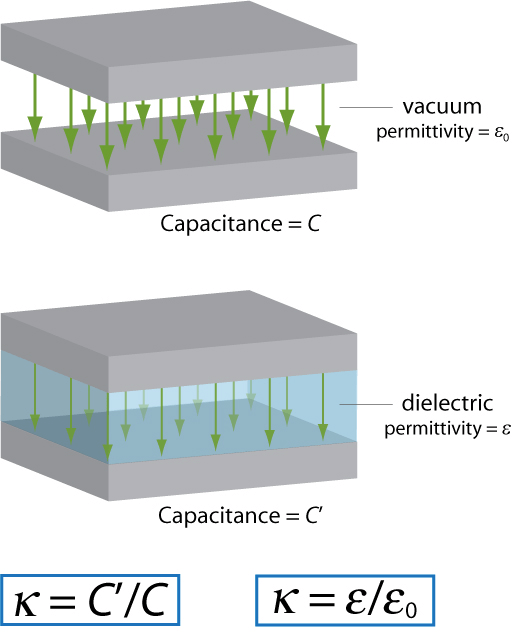
Dielectric Constant (κ)

Example 4: Capacitors in Series

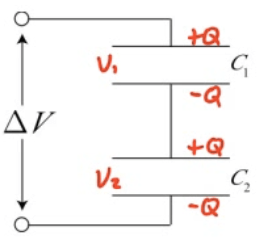
• Determine the equivalent capacitance of two capacitors in series

• 

• 

  

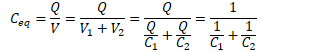
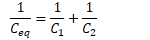
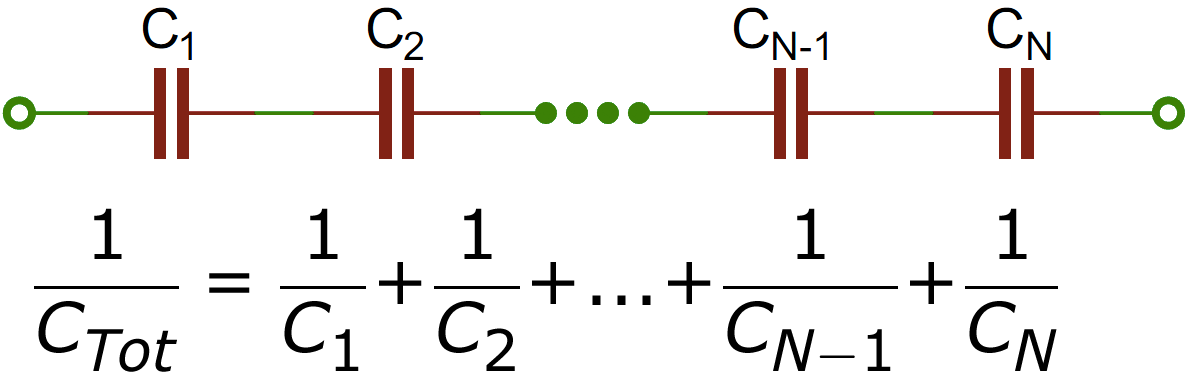
Example 5: Capacitors in Parallel

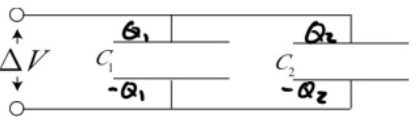
• Determine the equivalent capacitance of two capacitors in parallel

• 

  

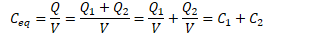
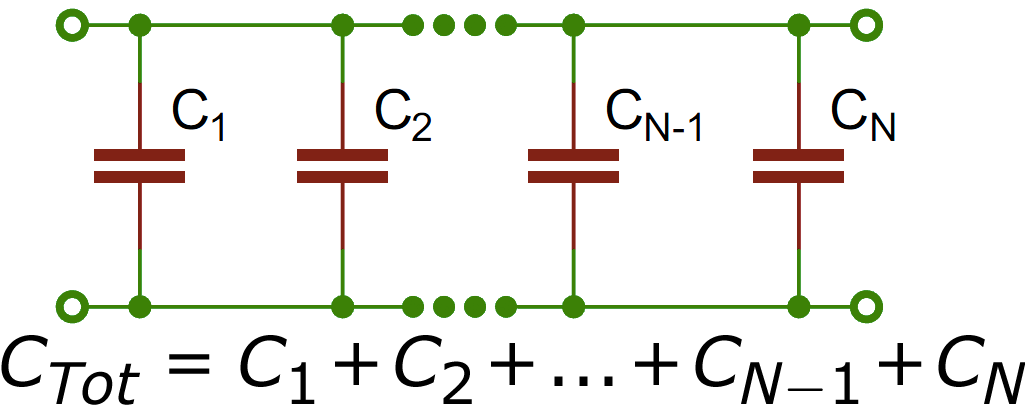
Example 6: Capacitance

• A capacitor stores 3 microcoulombs of charge with a potential difference of 1.5 volts across the plates. What is its capacitance? How much energy is stored in the capacitor?

• 

• 

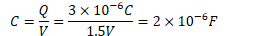
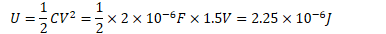
Example 7: Charge on a Capacitor

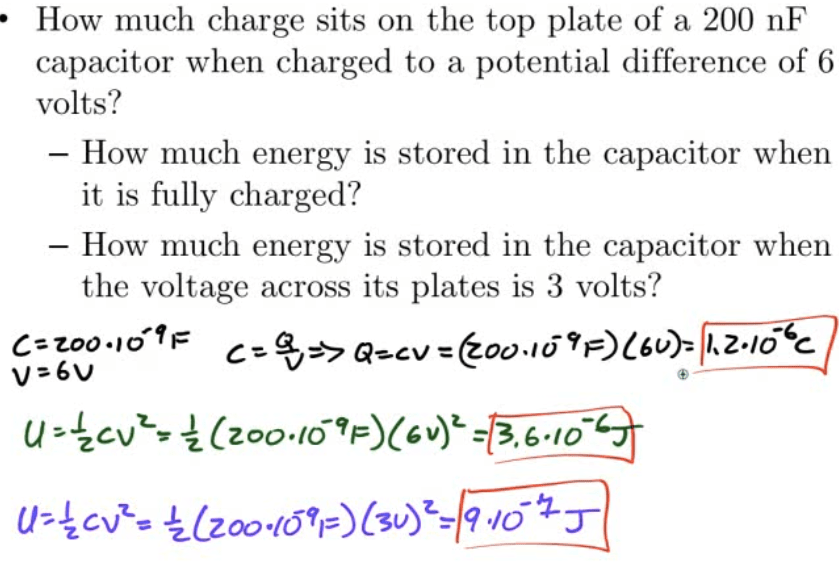
Example 8: Designing a Capacitor

Example 9: Calculating Capacitance

Example 10: Two Conducting Spheres

Example 11: Inserting a Dielectric